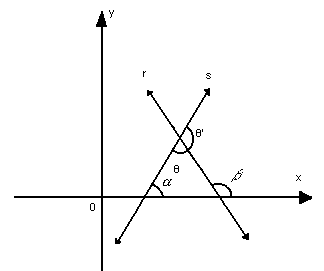
Ângulo entre duas retas

Sendo r e s duas retas não-verticais e não-perpendiculares entre si, pelo teorema do ângulo externo , temos:

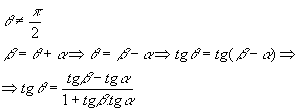
Dependendo da posição das duas retas no plano, o ângulo pode ser agudo ou obtuso. Logo:

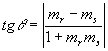
Essa relação nos fornece o ângulo agudo entre r e s, pois . O ângulo obtuso será o suplemento de .