Você está em Ensino médio > Geometria analítica - Retas ▼
📄 Introdução
📄 Plano cartesiano
📄 Distância entre dois pontos
📄 Razão de secção
📄 Ponto médio
📄 Baricentro de um triângulo
📄 Condições de alinhamento de três pontos
📄 Equação geral
📄 Equação segmentária
📄 Equações paramétricas
📄 Equação reduzida
📄 Coeficiente angular
📄 Representação gráfica de retas
📄 Posições relativas entre retas
📄 Ângulo entre duas retas
📄 Distância entre ponto e reta
📄 Bissetrizes
📄 Plano cartesiano
📄 Distância entre dois pontos
📄 Razão de secção
📄 Ponto médio
📄 Baricentro de um triângulo
📄 Condições de alinhamento de três pontos
📄 Equação geral
📄 Equação segmentária
📄 Equações paramétricas
📄 Equação reduzida
📄 Coeficiente angular
📄 Representação gráfica de retas
📄 Posições relativas entre retas
📄 Ângulo entre duas retas
📄 Distância entre ponto e reta
📄 Bissetrizes
Distância entre dois pontos
Dados os pontos A(xA, yA) e B(xB, yB) e sendo dAB a distância entre eles, temos:
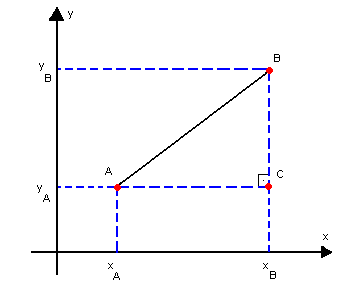
![]()
Aplicando o teorema de Pitágoras ao triângulo retângulo ABC, vem:
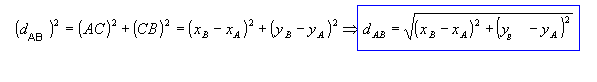
Como exemplo, vamos determinar a distância entre os pontos A(1, -1) e B(4, -5):
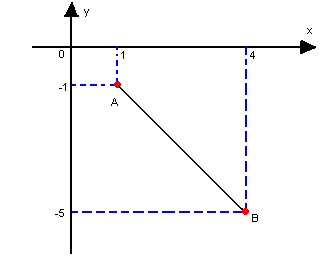
![]()
Próximo: Razão de secção
Como referenciar: "Geometria analítica - Retas" em Só Matemática. Virtuous Tecnologia da Informação, 1998-2025. Consultado em 03/04/2025 às 06:35. Disponível na Internet em https://www.somatematica.com.br/emedio/retas/retas1_2.php





























