Secção e áreas do prisma

Um plano que intercepte todas as arestas de um prisma determina nele uma região chamada secção do prisma.

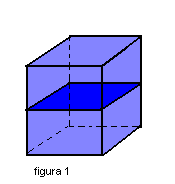
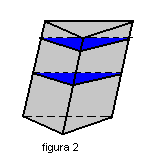
Secção transversal é uma região determinada pela intersecção do prisma com um plano paralelo aos planos das bases (figura 1). Todas as secções transversais são congruentes (figura 2).

Áreas

Em um prisma, distinguimos dois tipos de superfície: as faces e as bases. Assim, temos de considerar as seguintes áreas:

a) área de uma face (A_F ): área de um dos paralelogramos que constituem as faces;

b) área lateral (A_L): soma das áreas dos paralelogramos que formam as faces do prisma.

No prisma regular, temos:

A_L = n . A_F (n = número de lados do polígono da base)

c) área da base (A_B): área de um dos polígonos das bases;

d) área total (A_T): soma da área lateral com a área das bases.

A_T = A_L + 2A_B

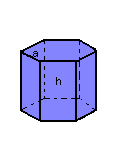
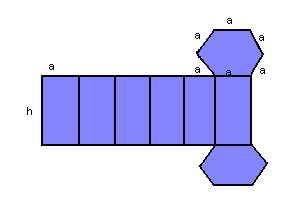
Vejamos um exemplo. Dado um prisma hexagonal regular de aresta da base a e aresta lateral h, temos: