|
Geometria
Espacial
Pirâmides
Dados um polígono convexo R, contido em um plano  ,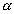
e um ponto V ( vértice) fora de ,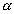
chamamos de pirâmide o conjunto de todos os segmentos  .
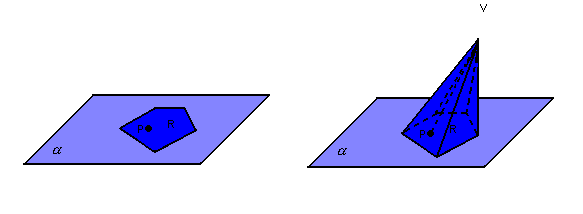
Elementos da pirâmide
Dada a pirâmide a seguir, temos os seguintes elementos:
-
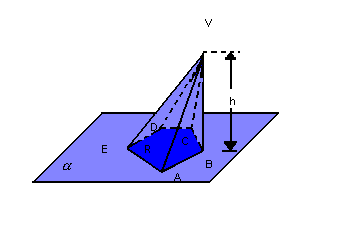
base: o polígono convexo R
-
arestas da base: os lados 
do polígono
-
arestas laterais: os segmentos 
-
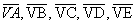faces laterais: os triângulos VAB, VBC,
VCD, VDE, VEA
-
altura: distância h do ponto V
ao plano
Classificação
Uma
pirâmide é reta quando a projeção ortogonal do vértice coincide com o
centro do polígono da base.
Toda pirâmide reta, cujo polígono da base é regular, recebe o nome de pirâmide
regular. Ela pode ser triangular, quadrangular, pentagonal etc., conforme
sua base seja, respectivamente, um triângulo, um quadrilátero, um pentágono
etc.
Veja:
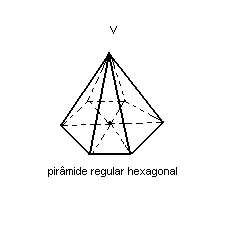
Observações:
1ª) Toda pirâmide triangular recebe o nome
do tetraedro. Quando o tetraedro possui como faces triângulos eqüiláteros,
ele é denominado regular ( todas as faces e todas as arestas são congruentes).
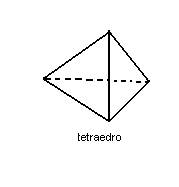
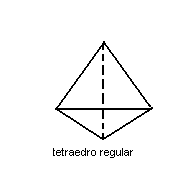
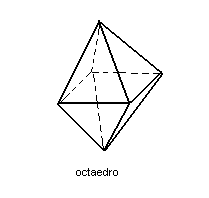
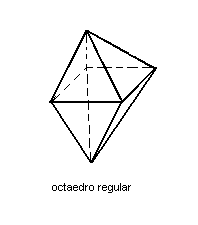
2ª) A reunião, base com base, de duas pirâmides
regulares de bases quadradas resulta num octaedro. Quando as faces das
pirâmides são triângulos eqüiláteros, o octaedro é regular.
<<
Voltar para seção Ensino médio
|
