Área e volume do cone

Área

Desenvolvendo a superfície lateral de um cone circular reto, obtemos um setor circular de raio g e comprimento :

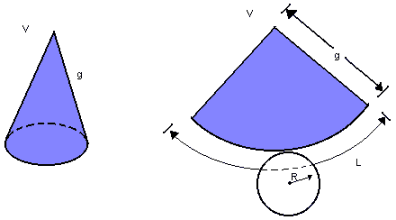
Assim, temos de considerar as seguintes áreas:

a) área lateral (A_L): área do setor circular.

b) área da base (A_B): área do circulo do raio R.

c) área total (A_T): soma da área lateral com a área da base.

Volume

Para determinar o volume do cone, vamos ver como calcular volumes de sólidos de revolução. Observe a figura:

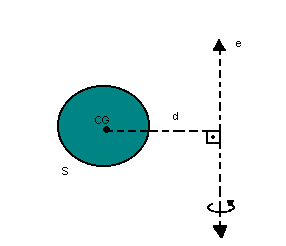
d = distância do centro de gravidade (CG) da sua superfície ao eixo e

S=área da superfície

Sabemos, pelo Teorema de Pappus-Guldin, que, quando uma superfície gira em torno de um eixo e, gera um volume tal que:

Vamos então determinar o volume do cone de revolução gerado pela rotação de um triângulo retângulo em torno do cateto h:

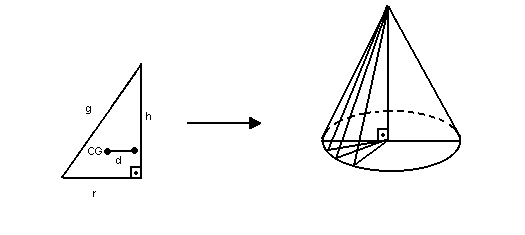
O CG do triângulo está a uma distância  do eixo de rotação. Logo: