|
Geometria
Espacial
Ângulo poliédrico
Sejam
n  semi-retas de
mesma origem tais que nunca fiquem três num mesmo semiplano. Essas semi-retas
determinam n ângulos em que o plano de cada um deixa as outras
semi-retas em um mesmo semi-espaço. A figura formada por esses ângulos é o ângulo
poliédrico.
Poliedros
Chamamos
de poliedro o sólido limitado por quatro ou mais polígonos planos,
pertencentes a planos diferentes e que têm dois a dois somente uma aresta em
comum. Veja alguns exemplos:
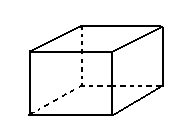
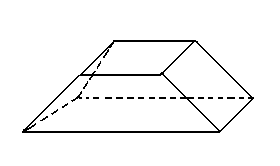
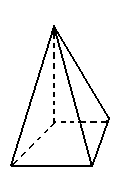
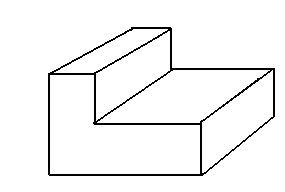
Os polígonos
são as faces do poliedro; os lados e os vértices dos polígonos são as
arestas e os vértices do poliedro.
Poliedros
convexos e côncavos
Observando os poliedros acima,
podemos notar que, considerando qualquer uma de suas faces, os poliedros
encontram-se inteiramente no mesmo semi-espaço que essa face determina. Assim,
esses poliedros são denominados convexos.
Isso não acontece no último poliedro, pois, em relação a duas de suas faces,
ele não está contido apenas em um semi-espaço. Portanto, ele é denominado
côncavo.
Classificação
Os poliedros convexos possuem nomes especiais de acordo com o número de faces,
como por exemplo:
-
tetraedro:
quatro faces
-
pentaedro: cinco faces
-
hexaedro: seis faces
-
heptaedro: sete faces
-
octaedro: oito faces
-
icosaedro: vinte faces
<<
Voltar para seção Ensino médio
|
