Posições relativas de dois planos

Consideramos as seguintes situações:

a) planos coincidentes ou iguais

b) planos concorrentes ou secantes

Dois planos, , são concorrentes quando sua intersecção é uma única reta:

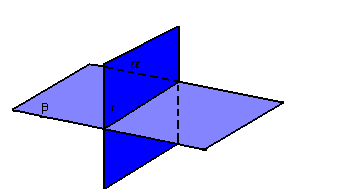
c) planos paralelos

Dois planos, , são paralelos quando sua intersecção é vazia:

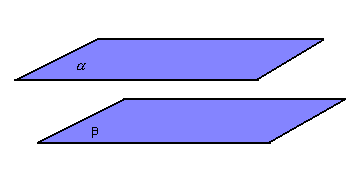
Perpendicularismo entre planos

Dois planos, , são perpendiculares se, e somente se, existe uma reta de um deles que é perpendicular ao outro:

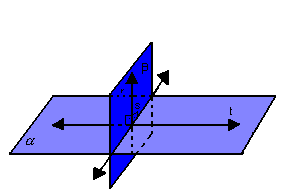
Observação: Existem infinitos planos perpendiculares a um plano dado; esses planos podem ser paralelos entre si ou secantes.