📄 Axiomas
📄 Posições relativas de duas retas
📄 Determinação de um plano
📄 Posições relativas de reta e plano
📄 Perpendicularismo entre reta e plano
📄 Posições relativas de dois planos
📄 Projeção ortogonal
📄 Distâncias entre ponto, reta e planos
📄 Ângulos entre retas e planos
📄 Diedros, triedos, poliedros
📄 Poliedros
📄 Poliedros regulares
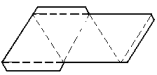
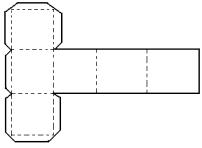
📄 Prismas
📄 Classificação dos prismas
📄 Secção do prisma
📄 Paralelepípedo
📄 Cubo
📄 Generalização do volume de um prisma
📄 Cilindro
📄 Secções do cilindro
📄 Área e volume do cilindro
📄 Cilindro equilátero
📄 Cone circular
📄 Área e volume do cone
📄 Pirâmide
📄 Secção paralela à base de uma pirâmide
📄 Área e volume da pirâmide
📄 Tronco de pirâmide
📄 Tronco de cone
📄 Esfera
📄 Partes da esfera
Poliedros regulares
Um poliedro convexo é chamado de regular se suas faces são polígonos regulares, cada um com o mesmo número de lados e, para todo vértice, converge um mesmo número de arestas.
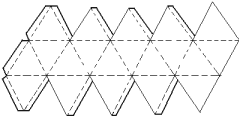
Existem cinco poliedros regulares, que são apresentados a seguir:
|
Poliedro |
Planificação |
Elementos |
|
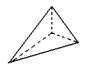
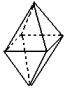
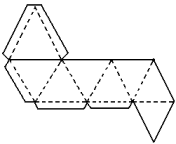
Tetraedro |
|
4 faces triangulares 4 vértices 6 arestas |
|
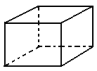
Hexaedro |
|
6 faces quadrangulares 8 vértices 12 arestas |
|
Octaedro |
|
8 faces triangulares 6 vértices 12 arestas |
|
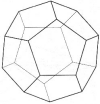
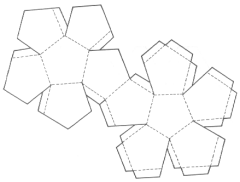
Dodecaedro |
|
12 faces pentagonais 20 vértices 30 arestas |
|
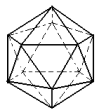
Icosaedro |
|
20 faces triangulares 12 vértices 30 arestas |
Relação de Euler
Em todo poliedro convexo é válida a relação seguinte:
V - A + F = 2
em que V é o número de vértices, A é o número de arestas e F, o número de faces. Observe os exemplos:
V=8 A=12 F=6 8 - 12 + 6 = 2 |
V = 12 A = 18 F = 8 12 - 18 + 8 = 2 |
Poliedros platônicos
Diz-se que um poliedro é platônico se, e somente se:
a) for convexo;
b) em todo vértice concorrer o mesmo número de arestas;
c) toda face tiver o mesmo número de arestas;
d) for válida a relação de Euler.
Assim, nas figuras acima, o primeiro poliedro é platônico e o segundo, não-platônico.