Posições relativas de reta e plano

Vamos considerar as seguintes situações:

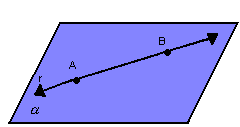
a) reta contida no plano: se uma reta r tem dois pontos distintos num plano , então r está contida nesse plano:

b) reta concorrente ou incidente ao plano: dizemos que a reta r "fura" o plano ou que r e são concorrentes em P quando .

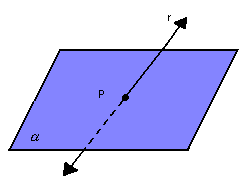
Observação: a reta r é reversa a todas as retas do plano que não passam pelo ponto P.

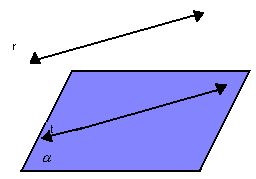
c) reta paralela ao plano: se uma reta r e um plano não têm ponto em comum, então a reta r é paralela a uma reta t contida no plano ; portanto, r // .

Em existem infinitas retas paralelas, reversas ou ortogonais a r.

P₁₁) Se dois planos distintos têm um ponto em comum, então a sua intersecção é dada por uma única reta que passa por esse ponto.