Regressão simples (RLS)

Em inúmeras problemáticas, o pesquisador depara-se com duas varáveis que proporcionam previsão de comportamentos futuros.

Esta previsão pode ser alcançada através de um estudo que envolve a equação da reta de regressão, concebida através das variáveis critério (y, dependente ou de resposta) e a independente (x, também conhecida como prognóstico).

Trata-se de uma realidade comum no universo da pesquisa, envolvendo variáveis como renda, idade, gastos, entre muitas outras.

Equação da reta

Y = a₁ + a₂.x

Onde, y é a variável dependente e x a independente.

a₁ é o valore de y para x e a₂.é valor médio de y por unidade x.

A relação linear entre as duas variáveis é medida pelo coeficiente de correlação (R).

R varia de –1 a 1, onde 1 é a correlação perfeita e o oposto indica forte correlação negativa. Valores próximos de zero indicam fraca correlação.

No exemplo abaixo, se existisse um R elevado poderia-se prever y para eventos futuros.

O cálculo de R é uma operação bastante simples para softwares com funções estatísticas, sendo desnecessário o aprofundamento dos procedimentos de calculo.

Neste tipo de análise é importante determinar o quanto a linha de regressão representa os dados. Neste caso, se faz necessário calcular o R² de Pearson ou coeficiente de determinação.

Um R²  igual a 0,80, tem-se que 80% da variabilidade decorre de x. Inversamente, pode-se dizer que 20% da variância de Y não é atribuível às diferenças em x.

Para obter-se o teste de hipótese, formula-se H₀ e H₁ da seguinte forma:

H₀ :p = 0

H₁: p ≠ 0

O cálculo de t é realizado através da formula,

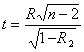
Sendo t calculado maior do que t tabelado, rejeita-se a hipótese nula.

Exemplo

Um motorista deseja prever seus gastos com seu automóvel em função dos quilômetros que roda por mês.

Observando a tabela acima, percebe-se uma forte correlação entre as variáveis, onde R está muito próximo de 1.