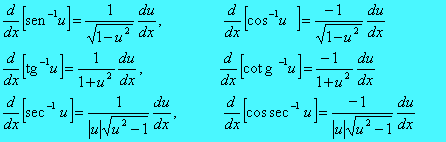|
Funções
Logarítmica e Exponencial
DERIVADAS
DAS FUNÇÕES TRIGONOMÉTRICAS INVERSAS
Um problema comum em trigonometria é achar um
ângulo cujas funções trigonométricas são conhecidas. Problemas deste tipo
envolvem a computação de funções arco, tais como arcsen x,
arccos x, arctg x, e assim por diante. Consideremos esta idéia do
ponto de vista de funções inversas, com a meta de desenvolver fórmulas de
derivadas para as funções trigonométricas inversas.
- IDENTIDADES PARA FUNÇÕES TRIGONOMÉTRICAS
INVERSAS
Se interpretamos 
x como um
ângulo medido em radianos cujo seno é x, e se aquele ângulo for não
negativo, então podemos representar x como um ângulo em um
triângulo retângulo, no qual a hipotenusa tem comprimento 1 e o lado oposto ao
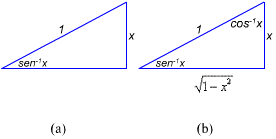
ângulo de
tem comprimento x (figura a).
Pelo Teorema de Pitágoras, o lado adjacente para o
ângulo tem comprimento  . Além
disso, a ângulo oposto a
é  ,
uma vez que o co-seno daquele ângulo é x (figura b). Este triângulo
motiva várias identidades úteis, envolvendo funções trigonométricas que
são válidas para 
. Por exemplo:
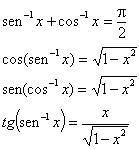
Analogamente,  x e
x podem ser representadas
com ângulos de triângulos retângulos mostrados na figura c e d.
Esses
triângulos revelam mais identidades úteis, como por exemplo:
 
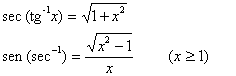
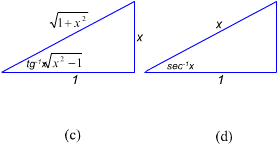
OBSERVAÇÃO. Não
se ganha nada memorizando estas identidades; o que é importante é compreender
o método usado para obtê-las.
Exemplo
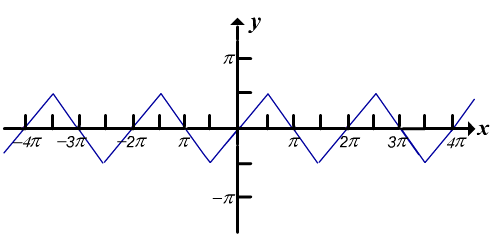
A figura abaixo mostra um gráfico gerado por um
computador de y = (sen x). Pode se pensar
que este gráfico deva ser a reta y = x, uma vez que (sen
x) = x. Por que isto não acontece?
Solução. A
relação (sen x) = x é válida no
intervalo  ; logo podemos dizer, com certeza, que os gráficos de y = (sen
x) e y = x coincidem neste intervalo. Contudo, fora deste
intervalo, a relação
(sen
x) = x não precisa ser válida. Por
exemplo, se estiver no
intervalo  , então a
quantidade x - 
estará no intervalo .
Assim
Desta forma,usando a identidade sen(x-)
= -sen x e o fato de que
é uma função ímpar, podemos
expressar
(sen
x) como
Isso mostra que no
intervalo , o
gráfico de y =
(sen x) coincide com a reta y = -(x-),
a qual tem inclinação -1 e um intercepto x em x = ,
o que está de acordo com a figura.
- DERIVADAS DE FUNÇÕES TRIGONOMÉTRICAS INVERSAS
Lembre-se que se f for uma função um a um, cuja a
derivada é conhecida, então há duas maneiras básicas para obter uma fórmula
de derivação para  (x), podemos reescrever a equação
y = (x) como x = f(y), e diferenciar
implicitamente. Usaremos a diferenciação implícita para obter a fórmula de
derivação para y = 
x. Reescrevendo esta
equação como x = sen y e diferenciando implicitamente,
obtemos
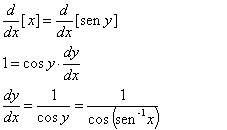
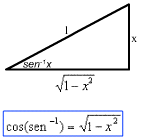
Esta fórmula de derivada pode ser simplificada
aplicando-se a fórmula  , que foi deduzida a partir do triângulo da
figura, resultando:
Assim, mostramos que
Se u for uma função diferenciável de x,
então
e a regra da cadeia produzem a seguinte fórmula generalizada
da derivada
O método usado para obter esta fórmula pode também
ser usado para obter fórmulas generalizadas de derivadas para outras funções
trigonométricas inversas. Estas fórmulas, válidas para -1< u < 1, são
<<
Voltar para Ensino Superior
|
