Funções definidas explicitamente e implicitamente

Até agora, estávamos preocupados em diferenciar funções que são expressas na forma y = f (x). Dizemos que uma equação desta forma define y explicitamente como uma função de x, pois a variável y aparece sozinha de um lado da equação. Entretanto, algumas vezes as funções estão definidas com equações nas quais y não está sozinho de um lado; por exemplo, a equação

yx  + y +1 = x

não está na forma y = f (x). Contudo, esta equação ainda define y como uma função de x, uma vez se pode reescrever como

     y = 

Assim dizemos que xy  + y +1 = x define y implicitamente como uma função de x, sendo

     f (x) = 

Uma equação em x e y pode implicitamente definir mais do que uma função de x; por exemplo, se resolvermos a equação

para y em termos de x, obtemos ; assim, encontramos duas funções que estão definidas implicitamente por , isto é

          e            

Os gráficos destas funções são semicírculos superiores e inferiores do círculo  .

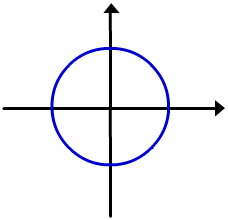
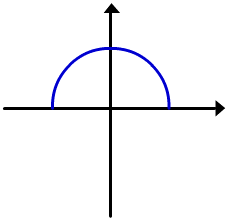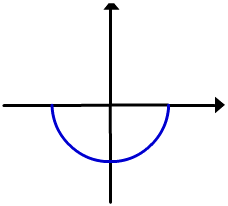y=

y = -

Em geral, se tivermos uma equação em x e y, então qualquer segmento de seu gráfico que passe pelo teste vertical pode ser visto como gráfico de una função definida pela equação. Assim fazemos a seguinte definição:

  Assim, por exemplo, a equação define as funções e implicitamente, uma vez que os gráficos dessas funções são os segmentos do círculo .

Às vezes, pode ser difícil ou impossível resolver uma equação em x e y para y em termos de x.

Com persistência, a equação

por exemplo, pode ser resolvida para y em termos de x, mas a álgebra é enfadonha e as fórmulas resultantes são complicadas. Por outro lado, a equação 

  sen(xy) = y

não pode ser resolvida para y em termos de x por qualquer método elementar. Assim, mesmo que uma equação em x e y possa definir uma ou mais funções de x, pode não ser prático ou possível achar fórmulas explícitas para aquelas funções.