Logaritmos

Lembre-se que, algebricamente, o logaritmo é um expoente. Mais precisamente, se b > 0 e b 1, então para valores positivos de x o logaritmo na base b de x é denotado por    

e é definido como sendo aquele expoente ao qual b deve ser elevado para produzir x. Por exemplo,

Historicamente, os primeiros logaritmos a serem estudados foram os de base 10 chamados de logaritmos comuns. Para tais logaritmos, é usual suprimir referência explícita para a base e escrever log x e não . Mais recentemente, os logaritmos de base dois desempenharam importante papel em ciência computacional, uma vez que surgem naturalmente em sistema numérico binário.

Porém, os logaritmos mais largamente usados nas aplicações são logaritmos naturais, os quais tem uma base natural denotada pela letra e em homenagem ao matemático suíço Leonard Euler, que primeiro sugeriu sua aplicação aos logaritmos no artigo não-publicado, escrito em 1728. Esta constante, cujo valor está em seis casas decimais, é

e2, 718282

surge como assíntota horizontal ao gráfico da equação

y =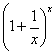

Os valores deaproximam-se a e

x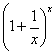
1	2	2,000000
10	1,1	2,593742
100	1,01	2,704814
1000	1,001	2,716924
10.000	1,0001	2,718146
100.000	1,00001	2,718268
1.000.000	1,000001	2,718280

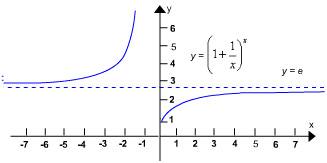
O fato de que y = e, quando x e quando x é expresso pelos limites

  e   

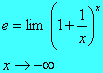
A função exponencial f (x) = é chamada de função exponencial natural. Para simplificar a tipografia, esta função é, algumas vezes, escrita como exp x. Assim, por exemplo, você pode ver a relação expressa como

exp(+) = exp() exp()

Esta notação é também usada por recursos computacionais, e é típico acessar a função com alguma variação do comando EXP.